|
|
|
|
|
|
|
|
| Dozent: | Prof. Dr. Ernst W. Mayr |
| Zeit: |
Vorlesung Montag 10:15 - 12:00 (erster Termin: 11.5.98), 4 Stunden Lösen der Programmieraufgaben (6 SWS) |
| Raum: | Vorlesung im Raum S2229, Lösen der Programmieraufgaben im Rechnerraum S2221 |
| Bereich: |
Informatik I (alte Prüfungsordnung) Informatik III (neue Prüfungsordnung) (Details hier) |
| Voraussetzungen: | bestandenes Vordiplom; Besuch der Veranstaltung Effiziente Algorithmen I, II empfehlenswert |
| Praktikumsleiter: | Thomas Erlebach |
| Anmeldung: | zentrale Einschreibung in der HP-Halle |
| Scheinerwerb: | unbenoteter Schein für Lösen aller Programmieraufgaben (in Zweiergruppen; Erreichen einer gewissen Mindestpunktzahl ist notwendig) und mündliche Prüfung am Semesterende |
Viele Probleme, die in der Praxis auftreten, lassen sich sehr gut mit Hilfe von Graphen modellieren und lösen. Aus diesem Grund beschäftigen sich seit mehreren Jahrzehnten Wissenschaftler aus den Bereichen Informatik und Mathematik intensiv mit der Entwicklung von Algorithmen zur effizienten Lösung typischer Problemstellungen für Graphen. Dabei hat sich gezeigt, daß es für viele Probleme, bei denen ein naiver Lösungsansatz zu exponentiellen Laufzeiten führt, doch sehr schnelle Algorithmen gibt.
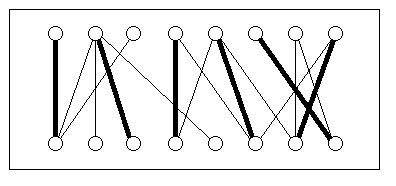
Ein Beispiel sind sogenannte Matching-Algorithmen, die viele unterschiedliche Zuordnungsprobleme lösen können. Ein solches Problem könnte etwa darin bestehen, Dozenten und Kurse einander so zuzuordnen, daß möglichst viele Kurse gehalten werden können. Dabei soll jeder Dozent nur einen Kurs halten, und jeder Kurs soll nur von einem Dozenten gehalten werden. In diesem Fall läßt sich das Problem als bipartiter Graph modellieren (siehe Bild). Die obere Reihe von Knoten entspricht den Dozenten, die untere Reihe den Kursen. Eine Kante zwischen einem Dozent und einem Kurs bedeutet, daß der Dozent fähig ist, den Kurs zu halten. Eine unter diesen Bedingungen gültige Zuordnung von Dozenten zu Kursen entspricht genau einem Matching. Im Beispiel können maximal sechs der acht Kurse gehalten werden, und die fett dargestellten Kanten entsprechen einer solchen Zuordnung. Der Algorithmus von Hopcroft und Karp löst das Matching-Problem in bipartiten Graphen in Zeit O(sqrt(n)*m), wobei n die Anzahl der Knoten und m die Anzahl der Kanten des Graphen ist.
Neben ihrer Nützlichkeit für die Lösung praktischer Probleme sind Graphenalgorithmen vor allem auch aufgrund der eingesetzten algorithmischen Techniken und der verwendeten Datenstrukturen interessant. Student(inn)en, die an dem Praktikum teilnehmen wollen, sollten daher die Bereitschaft haben, sich auch in kompliziertere Algorithmen hineinzudenken.
|
|
Tiefensuche, Breitensuche |
|
|
Zusammenhangskomponenten |
|
|
Minimale Spannbäme |
|
|
Kürzeste Pfade |
|
|
Matchings |
|
|
Netzwerkfluß |
|
|
Färbung planarer Graphen |
|
|
Approximation des Traveling Salesman Problem |
Neben diesen Graphenproblemen werden aber auch einige Probleme behandelt, die aus einem anderen Anwendungsbereich kommen und nur indirekt mit Graphen zu tun haben. Beispiele hierfür sind:
|
|
Suchen von Strings in Texten |
|
|
Berechnung der Edit-Distance zweier Strings |
Viele der Algorithmen werden in den Vorlesungen "Effiziente Algorithmen und Datenstrukturen" und "Effiziente Algorithmen und Datenstrukturen II" besprochen. Der Besuch dieser Vorlesungen ist empfehlenswert, aber nicht unbedingt erforderlich. Im Rahmen einer speziellen zweistündigen Praktikumsvorlesung werden die zum Verständnis der Funktionsweise der Algorithmen und zur Implementierung notwendigen Grundlagen erklärt. Korrektheitsbeweise und Laufzeitanalysen können dabei aus Zeitgründen aber oft nicht besprochen werden; diese können aber meist in den Vorlesungen "EA I" und "EA II" gehört werden.
Das Praktikum soll ein tieferes Verständnis für die Arbeitsweise effizienter Algorithmen, insbesonde Graphenalgorithmen, vermitteln und den Student(inn)en die für effiziente Implementierungen notwendigen höheren Datenstrukturen nahebringen.
LEDA ist eine Klassenbibliothek, die häufig verwendete Datenstrukturen wie Stacks, Queues, Priority-Queues, Listen, Graphen usw. zur Verfügung stellt und damit eine große Erleichterung für C++-Programmierer bringt. Auch die Visualisierung von Graphenalgorithmen kann sehr komfortabel mittels der LEDA-Klasse GraphWin erfolgen.
Die Bearbeitung der Praktikumsaufgaben kann entweder auf unseren Lehrstuhl-Rechern (S 2221), in der HP-Halle (Vorsicht: Compilierung von LEDA-Programmen dauert sehr lange!) oder auch auf einem Linux-Rechner zu Hause erfolgen (in letzterem Fall muß dann LEDA auf dem Rechner installiert werden). Die Aufgaben sollen in Zweiergruppen bearbeitet werden, wobei wir dringend empfehlen, die Aufgaben nicht aufzuteilen, sondern wirklich in Zusammenarbeit zu lösen und zu implementieren. Bei der Prüfung am Ende des Praktikums wird erwartet, daß jede(r) Student(in) bei allen Praktikumsaufgaben auch zur Implementierung, die von seiner/ihrer Gruppe abgegeben wurde, Fragen beantworten kann.
Während des Praktikums findet einmal pro Woche eine zweistündige Vorlesung statt, bei der die neuen Aufgaben und die zu implementierenden Algorithmen erklärt werden. Ein Skript, das ziemlich genau dem Vorlesungsinhalt entspricht, wird von den Aufgabenstellern erstellt und zur Verfügung gestellt. Die Abgabe der Lösungen (Source-Codes) erfolgt per E-Mail an algoprak@hpmayr1.informatik.tu-muenchen.de. Die Lösungen werden von einem Betreuer korrigiert, der seine Kommentare und die Bewertung der Lösung dann ebenfalls per E-Mail den Student(inn)en mitteilt. Fragen der Student(inn)en bezüglich Algorithmen und etwaigen Problemen bei der Implementierung können entweder in der Praktikumsvorlesung oder direkt mit den Betreuern besprochen werden.
Die abgegebenen Lösungen werden nach den folgenden Kriterien beurteilt und mit einer Punktzahl bewertet.
Um den unbenoteten Praktikums-Schein zu erhalten, müssen die folgenden Kriterien erfüllt werden:
WICHTIG: Das Praktikum Algorithmen-Entwurf zählt nach der alten Prüfungsordnung als Wahlpflichtpraktikum im Bereich Informatik I (Praktische Informatik), nach der neuen Prüfungsordnung (gültig ab November 1996) aber im Bereich Informatik III (Theoretische Informatik). Student(inn)en, die nach der neuen Prüfungsordnung DHP machen müssen, können den Schein nicht als Praktikumsschein zu Informatik I verwenden. Student(inn)en, die zwischen alter und neuer Prüfungsordnung wählen dürfen, können den Schein wahlweise als Schein zu Informatik I oder zu Informatik III verwenden. Für Details hier clicken!
|
|
Turau. Algorithmische Graphentheorie. Addison Wesley, 1996 |
|
|
Gibbons. Algorithmic Graph Theory. Cambridge University Press, 1985 |
|
|
Mehlhorn. Data Structures and algorithms 2: Graph algorithms and NP-Completeness, Springer-Verlag, 1984 |
|
|
Papadimitriou, Steiglitz. Combinatorial Optimization: Algorithms and complexity. Prentice-Hall, 1982 |
|
|
Sedgewick. Algorithms. Addison-Wesley, 1988 |
|
|
Tarjan. Data Structures and Network Algorithms. SIAM, 1983 |
|
|
Reingold, Nievergelt, Deo. Combinatorial Algorithms. Prentice-Hall, 1977 |
|
|
Ahuja, Magnanti, Orlin. Network Flows: Theory, Algorithms, and Applications. Prentice Hall, 1993. |